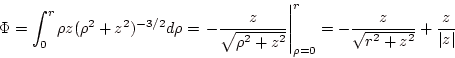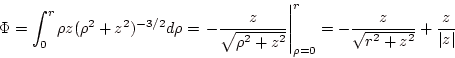

: 多重極場
: 軸回転対称場の場合
: 軸回転対称場の場合
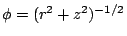 、
、
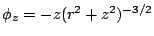 、
、
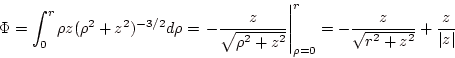 |
(1.11) |
「定数項」である第2項を省けば
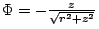 。
。
図 1.8:
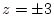 、
、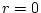 に符号が反対の点電荷が1つずつ。
に符号が反対の点電荷が1つずつ。
|
|
gnuplot> set contour base
gnuplot> unset surface
gnuplot> set view 0,0
gnuplot> set size square
gnuplot> set isosample 100
gnuplot> unset key
gnuplot> mf(r,z)=z/sqrt(r**2+z**2)
gnuplot> set cntrparam levels incremental -1.9,0.2,0
gnuplot> splot mf(x,y-3)-mf(x,y+3)
gnuplot> set term postscript enhanced color eps
Terminal type set to 'postscript'
Options are 'eps enhanced color colortext \
dashed dashlength 1.0 linewidth 1.0 defaultplex \
palfuncparam 2000,0.003 \
butt "Helvetica-Ryumin" 14'
gnuplot> set output "2pointcharges3d.eps"
gnuplot> replot
Morinaga Makoto
平成20年12月18日