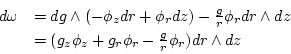

: 点電荷
: 電気力線・磁力線の描き方
: 重極場
スカラーポテンシャルを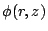 とする:
とする:
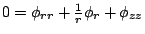 。
。
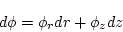 |
(1.6) |
これに直交する1次形式は
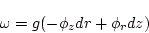 |
(1.7) |
であるが、
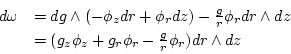 |
(1.8) |
なので、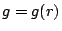 、
、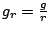 のときに一般に
のときに一般に
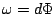 となる関数
となる関数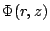 が
存在する。すなわち
が
存在する。すなわち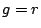 、
、
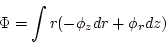 |
(1.9) |
積分路を
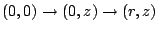 と取ると
と取ると
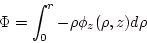 |
(1.10) |
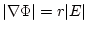 だから等高線プロットの線密度は
だから等高線プロットの線密度は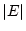 ではなく
ではなく
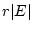 に比例するので
に比例するので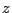 軸の近くでは線が疎らになり不自然に感じ
られるが
軸の近くでは線が疎らになり不自然に感じ
られるが
- 平面上で線の密度が
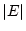 に比例するように描くことは不可能
(ある場所で比例するように描いても線をたどっていくと他の場所では
そうならない)。
に比例するように描くことは不可能
(ある場所で比例するように描いても線をたどっていくと他の場所では
そうならない)。
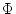 を等高線プロットしたものを
を等高線プロットしたものを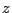 軸の回りで等間隔で
回転させると
軸の回りで等間隔で
回転させると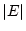 に比例した線密度が得られる。
に比例した線密度が得られる。
なので理屈的には「自然」なはず、だが。。。。
Morinaga Makoto
平成20年12月18日