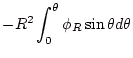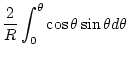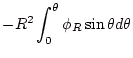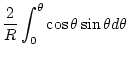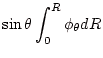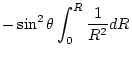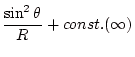

: 一様電界中の誘電体/導体球
: 多重極場
: 極座標
原点近傍の場は
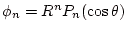 という形であった。
遠距離では
という形であった。
遠距離では
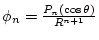 である。
1)
である。
1)
【例】双極子場(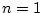 )の場合
)の場合
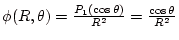 。最初の公式では
。最初の公式では
2番目の公式では
このように原点が特異点の場合は2番目の公式は使わないほうがいい
(例えば原点に裸の電荷がある場合は実際誤った結果を与える)。
図 1.10:
双極子が作る電場。赤が電気力線、緑が等電位面。縦軸が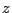 、
横軸が
、
横軸が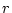 。
。
|
|
gnuplot> set size square
gnuplot> set xrange [-1:1]
gnuplot> set yrange [-1:1]
gnuplot> set style line 1 lt 1 lw 2
gnuplot> set style line 2 lt 2 lw 2
gnuplot> set polar
gnuplot> set samples 720
gnuplot> mf(t,a)=sin(t+pi/2)**2/a
gnuplot> mp(t,a)=sqrt(abs(cos(t+pi/2)/a))
gnuplot> plot mf(t,1) ls 1,mf(t,2) ls 1,mf(t,3) ls 1,mp(t,1) ls 2,
mp(t,2) ls 2,mp(t,3) ls 2
gnuplot> set output "dipole3d.eps"
gnuplot> set term postscript enhanced color eps
gnuplot> replot
Morinaga Makoto
平成20年12月18日