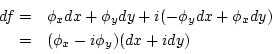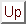

: 点電荷
: 電気力線・磁力線の描き方
: 電気力線・磁力線の描き方
スカラーポテンシャルを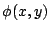 とする:
とする:
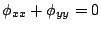 。電場は
。電場は
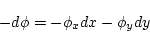 |
(1.1) |
これに直交する1次形式は
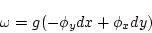 |
(1.2) |
であるが、
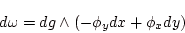 |
(1.3) |
なので、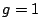 とすれば
とすれば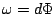 となる関数
となる関数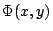 が
存在する:
が
存在する:
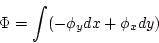 |
(1.4) |
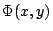 の等高線プロットが電気力線となる。
または
の等高線プロットが電気力線となる。
または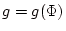 としてもよかったが、
としてもよかったが、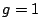 と取ると
と取ると
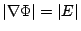 なので等高線の密度=電界の強さとなっていて都合がいい。
関数
なので等高線の密度=電界の強さとなっていて都合がいい。
関数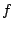 を
を
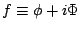 で定義する。
で定義する。
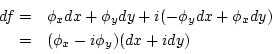 |
(1.5) |
だから(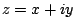 とおいて
とおいて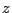 の関数として)
の関数として)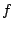 は解析関数である。
逆に
は解析関数である。
逆に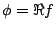 、
、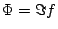 (
(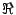 : Re,
: Re, 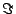 : Im)。
: Im)。
Morinaga Makoto
平成20年12月18日